Nicolò Vignatavan - Limits at infinity (ENG)

LIMITS AT INFINITY

Nicolò Vignatavan

-> Video

                     

[Throughout history, the concept of infinity has played a pivotal role in the game in which human

beings have always taken part against their unfulfilled thirst for knowledge. Philosophers,

mathematicians and poets of various eras have proposed their interpretation in this regard: 

Giordano Bruno proposed a testimony of faith; Kurt Godel, the proof of a logical incompleteness

and Giacomo Leopardi, overcoming finiteness (finitude). Today I will analyze the concept of

"infinity", reduced two-dimensionally on the Cartesian plane, comparing the trend of the

fundamental mathematical functions graphically by introducing the symbology of "plus infinity

minus".]

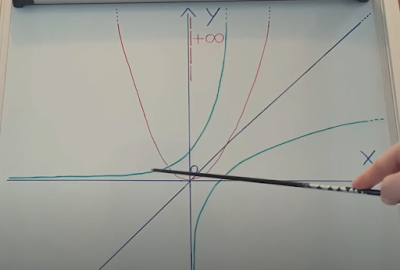
According to the theory of the hierarchy of infinities, taking into consideration the first

quadrant of the Cartesian plane, and, assuming one draws the graph of the function of an

increasing oblique straight line y = mx + q, of a parabolic function y = ax ^ 2, with term a> 0, of a

logarithmic function y = log (x) and of an exponential function y = a ^ x,

it is evident how the calculation of the limit for x which tends to + oo of all the

functions described above corresponds to + oo.

Always according to the theory of traditional mathematics, it is evident that the 4 functions

mentioned above do not tend towards + infinity with the same speed, but with a

displacement [delta (y)] different according to their intrinsic characteristics, although they

tend, on the whole, to + infinity, without stabilizing at any point value of y, along their path. It is

always evident that the order of growth rate towards y, in the first quadrant, for x tending to +

infinity, of the 4 functions is, from the fastest growing to the slowest growing, the following:

1st: exponential function, 2nd: parabolic function, 3rd: straight function, 4th: logarithmic function.

Let us assume the result + infinity of the calculation of the limit for x that tends to + oo, that of an

imaginary function that moves perfectly asymptotically towards the y axis.  If the result of the

calculation of the limit for x which tends to + infinity of the exponential function described above,

among the 4 functions considered is the one that comes closest to the characteristics of the

pure solution + oo of the imaginary function described above, or in other words it is the one

whose graphic path for x that tends to + oo moves more rapidly towards the y axis, then the

result of the limit will be considered as + oo ^ (-).  At this point, adding (-) at the apex of (+ oo) we

will have as results of the limits for x

which tends to + oo of the functions described above:

exponential function: + oo ^ (-)

parabolic function: + oo ^ (--)

linear function: + oo ^ (---)

logarithmic function: + oo ^ (----).